SETS: Stepwise Ensemble for Trade Selection Model

Overview

The Stepwise Ensemble for Trade Selection (SETS) model is a specialized predictive modeling approach built specifically to address challenges in trading system development. SETS automatically discovers patterns in historical strategy performance and creates an optimized ensemble of regression models to predict future market behavior. These models can be used as trade filters and position sizing optimizers in quantitative trading strategies, including the ones developed using MesoSim.

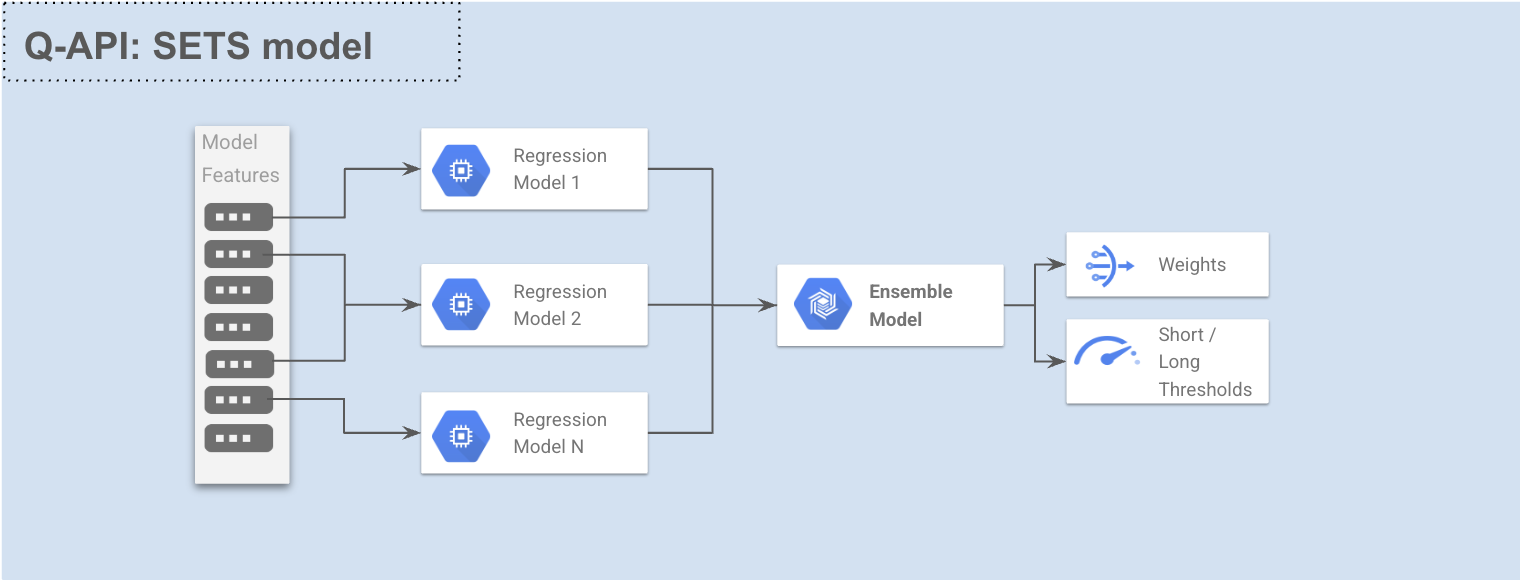
Unlike general-purpose statistical modeling packages, SETS is purpose-built for trading strategy analysis, combining the power of multiple specialist regression models into a robust ensemble that maximizes predictive performance while reducing the risk of overfitting.

Key Concepts

Predictive Modeling in Trading

Predictive modeling for trading relies on a fundamental property of strategy performance: markets and strategies contain patterns that tend to repeat throughout history and can often be used to predict future activity.

These patterns may include:

Trend continuation until exhaustion
Retracement toward recent mean price after a sudden move
Seasonal patterns and cyclical behavior

A predictive model studies historical strategy performance to discover these repeating patterns. Once identified, the model monitors for their reoccurrence and predicts whether the position to be taken will win, lose or break-even.

Features and Targets

SETS uses two key components for building predictive models:

Features: Variables derived from historical data (prices, volumes, open interest, IVs, Greeks and traditional indicators) that look strictly backward in time
Targets: Forward-looking variables that reveal strategy performance, represented as StrategyNAV fields for each Symbol/Strategy

The fundamental goal is to find relationships between features and targets that can be exploited for profitable trading. Trade decisions are made by comparing the model's predictions to optimized thresholds:

If the prediction exceeds an upper threshold, take a long position
If the prediction falls below a lower threshold, take a short position (or just ignore the entry)

How SETS Works

The SETS model consists of specialist regression models, each covering a subset of features (selected manually or automatically). These models are then combined into an ensemble when EnsembleMode is set to Average or Optimized. If EnsembleMode is set to Disabled, only one regression model is built.

SETS supports multiple regression types, covering various degrees of nonlinearity, including:

Linear Regression

Linear regression models the relationship between features and target using a linear equation:

y = β₀ + β₁x₁ + β₂x₂ + ... + βₙxₙ + ε

SETS uses multivariable linear regression, which many experts consider the best all-around modeling approach for trading systems because it is:

Fast to train
Powerful when given well-designed features
Less likely to overfit than nonlinear models, such as random forests or neural networks

Logistic Regression

Logistic regression transforms the continuous target variable into binary outcomes using the logistic function:

P(y=1) = 1 / (1 + e^(-(β₀ + β₁x₁ + ... + βₙxₙ)))

Logistic regression is similar to linear regression but designed for classification tasks. When the goal is to discriminate between two classes, logistic regression uses a binary target (zero or one) and is much more robust against outliers in the predictors compared to linear regression.

In logistic regression, SETS classifies position profits into Win or Loss buckets, then uses the classifier to predict trade outcomes (win/loss) based on the provided features.

Quadratic Regression

Quadratic regression extends the linear model by automatically generating squared terms and interaction features:

y = β₀ + β₁x₁ + β₂x₂ + β₃x₁² + β₄x₂² + β₅x₁x₂ + ε

In modeling tasks, there is an inherent tradeoff regarding the degree of nonlinearity. Linear models handle only straight-line relationships between the indicators and the target variable, reducing overfitting risk but ignoring curved effects.
At the other extreme, highly flexible methods (neural nets, decision trees) may capture rich structure yet are slower to train and prone to overfitting.

Quadratic (second-order polynomial) regression sits in the middle of this spectrum: it allows a single curvature (parabolic shape) in each predictor’s effect while keeping model complexity manageable. If a linear model under-performs, a quadratic one is typically the next step.

A quadratic model is essentially a linear model whose input set has been expanded with all squared terms and pairwise cross-products:

With one feature FEAT_1: FEAT_1, FEAT_1²
With two features FEAT_1, FEAT_2: FEAT_1, FEAT_2, FEAT_1², FEAT_1×FEAT_2, FEAT_2²
With three features: all original features plus their squares and all pairwise cross products

The number of terms grows rapidly as features increase, which could result in overfitting. However, quadratic regression remains much faster to train than most other nonlinear models while providing the flexibility to handle the majority of nonlinear relationships encountered in financial modeling.

Model Parameters

Basic Configuration

Parameter	Description
MinTimeInMarketPct	The minimum fraction (0-1) of training cases that must result in a trade being taken on each side. Reasonable values range from 0.05 to 0.20.
TargetMetric	The objective function to optimize for in models and ensemble. Options include RSquare, ROCArea, UlcerIndex, UlcerPerformanceIndex, ProfitFactor, LongProfitFactor, ShortProfitFactor.
CompressTargetOutliers	When enabled, performs monotonic compression on target's extreme values to mitigate the effect of outliers.
ModelRegressionType	The regression type of the model. Either `Linear`, `Quadratic` or `Logistic`

Feature Selection

Parameter	Description
ModelMaxFeatures	Maximum number of features to include in one model. When greater than zero, stepwise selection is enabled. When set to zero, all features are used.
ModelStepwiseMemory	The number of model parameters to remember during stepwise selection algorithm. Higher values check more combinations but increase computation time.
RegressionModelConfigs	A dictionary mapping model names to individual model configurations that can override global settings. Each model config can specify: Features (list of features to use), MaxFeatures, and StepwiseMemory. When not set, all features are used with global settings. Model names follow the scheme MODEL_{number}.

RegressionModelConfigs Details

The RegressionModelConfigs parameter allows fine-grained control over individual regression models within the ensemble. It's particularly useful when you want to create specialized models that focus on different feature sets.

Field	Type	Required	Description
Features	List<string>	No	An explicit list of features to use in this model. When specified, only these features will be considered for inclusion in the model, ignoring all other features in the dataset. If not provided, all available features will be used (filtered by the MaxFeatures parameter if set).
MaxFeatures	int	No	Maximum number of features to include in this specific model. When greater than zero, stepwise selection is enabled for this model. When set to zero, all specified features (or all available features if none specified) are used. If null, the global ModelMaxFeatures setting will be used.
StepwiseMemory	int	No	The number of model parameters to remember during stepwise selection algorithm for this specific model. Higher values check more combinations but increase computation time. If null, the global ModelStepwiseMemory setting will be used.
RegressionType	string	No	The regression type of the model. Either `Linear`, `Quadratic` or `Logistic`

Example Usage:

"RegressionModelConfigs": {
  "MODEL_0": {
    "Features": ["entry_pos_vega", "entry_pos_theta", "entry_leg_longs_iv"],
    "MaxFeatures": 2,
    "StepwiseMemory": 5,
    "RegressionType": "Linear"
  },
  "MODEL_1": {
    "Features": ["OEX_RSI_14", "SGX_RSI_7", "SPX_RSI_14"],
    "MaxFeatures": 3,
    "StepwiseMemory": 8,
    "RegressionType": "Quadratic"
  }
}

In this example:

MODEL_0 will only consider the 3 specified features and select at most 2 of them using stepwise selection with a memory of 5
MODEL_1 will only consider its 3 specified features and select at most 3 of them (all of them) using stepwise selection with a memory of 8

Using RegressionModelConfigs this way allows you to create specialized models focusing on different aspects of your trading system (e.g., one model for momentum indicators, another for volatility indicators).

Ensemble Configuration

Parameter	Description
EnsembleMode	Controls how multiple models are combined. Options: Disabled (one model), Average (equal weights), or Optimized (weights based on performance).
EnsembleModelCount	The number of models to create when ensemble mode is enabled.
EnsembleMaxModels	Maximum number of models to select for the ensemble using the stepwise algorithm.
EnsembleStepwiseMemory	Number of models to remember during stepwise selection for the ensemble.

Data Input

Parameter	Description
CsvContent	CSV data containing Features and Target.

Stepwise Selection Algorithm

By default, SETS uses forward stepwise selection for feature selection:

Each feature candidate is tested individually for performance
The best performer is selected first
Each remaining candidate is tested in combination with already selected features
The process continues until ModelMaxFeatures is reached or performance stops improving

To mitigate the primacy problem (where excellent feature combinations might be missed), ModelStepwiseMemory allows the algorithm to retain multiple promising feature sets instead of just the single best performer. This significantly improves the chances of finding optimal feature combinations.

Ensemble Methods

SETS supports three ensemble modes:

Disabled

Only a single model is built and used. Simple but may miss opportunities for improved performance through model combination.

Average

All models receive equal weight in the ensemble. This approach is least likely to overfit but treats all models as equally important regardless of their individual performance.

Optimized

Models are weighted based on their relative importance or quality, with two constraints:

No weight can be negative (avoiding prediction inversion)
Weights must sum to one (preventing correlated models from producing extreme weights)

This provides an excellent compromise between equal weighting and unconstrained optimization, allowing better models to have more influence while preventing overfitting.

Mitigating Outliers

Most models are sensitive to outliers, which can force the model to expend excessive effort learning to predict extreme cases at the expense of typical scenarios. Enabling CompressTargetOutliers applies a monotonic compressing function to the tails of the target distribution, reducing the impact of outliers while preserving order relationships.

Target Metrics

SETS supports multiple optimization metrics:

Metric	Description
RSquare	The fraction of the target variable's variance explained by the model. If R-square is optimized, the threshold for computing performance criteria is set at zero.
ROCArea	The area under the profit/loss ROC curve. A random model will have a value around 0.5, a perfect model 1.0.
ProfitFactor	Combines LongProfitFactor and ShortProfitFactor with simultaneously optimized thresholds.
LongProfitFactor	Optimizes for long positions by dividing the sum of positive target values by the sum of negative values for cases exceeding the threshold.
ShortProfitFactor	Similar to LongProfitFactor but optimized for short positions.
UlcerIndex	The square root of the mean squared drawdown. Available in long and short versions.
UlcerPerformanceIndex	Net change in equity divided by the Ulcer Index. Available in long and short versions.

Usage Example

{
  "MinTimeInMarketPct": 0.15,
  "TargetMetric": "ProfitFactor",
  "CompressTargetOutliers": true,
  "ModelMaxFeatures": 2,
  "ModelStepwiseMemory": 10,
  "RegressionModelConfigs": {
    "MODEL_0": {
      "Features": ["Feature1", "Feature2", "Feature3"],
      "MaxFeatures": 2,
      "StepwiseMemory": 8
    },
    "MODEL_1": {
      "Features": ["Feature4", "Feature5", "Feature6"],
      "MaxFeatures": 3,
      "StepwiseMemory": 10
    }
  },
  "EnsembleMode": "Optimized",
  "EnsembleModelCount": 5,
  "EnsembleMaxModels": 3,
  "EnsembleStepwiseMemory": 10,
  "CsvContent": "DateTime,Symbol,StrategyNAV,Feature1,Feature2,Feature3,Feature4,Feature5,Feature6\n2023-01-01,STRAT_0,1000,0.5,0.7,0.3,0.1,0.9,0.2\n2023-01-02,STRAT_0,1005,0.6,0.5,0.4,0.2,0.8,0.3\n..."
}

API Endpoint

POST /models/v1/sets

Request Format

The request requires a JSON body with the configuration parameters described above.

Response Format

The response contains the model results including weights for each feature in each model and the optimal thresholds:

{
  "Models": {
    "MODEL_0": {
      "Weights": {
        "Feature1": 0.45,
        "Feature2": 0.35,
        "CONSTANT": 0.11  
      },
      "LongThreshold": 0.15,
      "ShortThreshold": -0.12
    },
    "MODEL_1": {
      "Weights": {
        "Feature4": 0.25,
        "Feature5": 0.50,
        "CONSTANT": 0.25
      },
      "LongThreshold": 0.18,
      "ShortThreshold": -0.14
    },
    "ENSEMBLE": {
      "Weights": {
        "MODEL_0": 0.60,
        "MODEL_1": 0.40
      },
      "LongThreshold": 0.16,
      "ShortThreshold": -0.13
    }
  }
}

The trade direction is determined by comparing the model's prediction to the thresholds: Long position (or N times the normal allocation):

    ENSEMBLE.Weights.MODEL_0 * (Feature1 * MODEL_0.Weights.Weight1 + Feature2 * MODEL_0.Weights.Weight2 + MODEL_0.Weights.CONSTANT) + 
    ENSEMBLE.Weights.MODEL_1 * (Feature4 * MODEL_1.Weights.Weight4 + Feature5 * MODEL_1.Weights.Weight5 + MODEL_1.Weights.CONSTANT) > ENSEMBLE.LongThreshold

Short position (or ignored entry):

    ENSEMBLE.Weights.MODEL_0 * (Feature1 * MODEL_0.Weights.Weight1 + Feature2 * MODEL_0.Weights.Weight2 + MODEL_0.Weights.CONSTANT) + 
    ENSEMBLE.Weights.MODEL_1 * (Feature4 * MODEL_1.Weights.Weight4 + Feature5 * MODEL_1.Weights.Weight5 + MODEL_1.Weights.CONSTANT) < ENSEMBLE.ShortThreshold

When a single model is used (EnsembleMode is Disabled), the trade direction is determined by the model's prediction and thresholds:

    MODEL_0.Weights.Weight1 * Feature1 + MODEL_0.Weights.Weight2 * Feature2 + MODEL_0.Weights.CONSTANT > MODEL_0.LongThreshold

Notes and Limitations

The API currently supports up to 3069 features and 128 models
The model training process may take several minutes for large datasets
The HTTP Request body size is limited to 30MBs

Overview​

Key Concepts​

Predictive Modeling in Trading​

Features and Targets​

How SETS Works​

Linear Regression​

Logistic Regression​

Quadratic Regression​

Model Parameters​

Basic Configuration​

Feature Selection​

RegressionModelConfigs Details​

Ensemble Configuration​

Data Input​

Stepwise Selection Algorithm​

Ensemble Methods​

Disabled​

Average​

Optimized​

Mitigating Outliers​

Target Metrics​

Usage Example​

API Endpoint​

Request Format​

Response Format​

Notes and Limitations​